等效原理

等效原理在现代物理学中是非常重要的，它是1916年爱因斯坦建立的广义相对论的两个基本假设之一，另一个基本假设是广义相对性原理。等效原理又分为弱等效原理、强等效原理和甚强等效原理。

弱等效原理最初是伽利略通过对物体在引力场中规律的研究而得出的一个基本原理，因此它又叫做伽利略等效原理。可能大家对这个名词会感到有点陌生，但是相信大家在学习物理的时候都有听过这样一个故事：伽利略在比萨斜塔上同时释放了两个不同重量的小球，其结果是这两个小球几乎同时落地。如果用牛顿第二定律和万有引力定律来描述自由落体的时候，那么弱等效原理又可以表述为：“物体的惯性质量与引力质量之比是与物体的材料、重量等物理性质无关的常数。”如果我们选取适当的单位，比如使用国际单位，那么物体的惯性质量就和引力质量相等了。

强等效原理是对弱等效原理的扩展，这是爱因斯坦在提出广义相对论之时提出的，因此它又称为爱因斯坦等效原理。以封闭的电梯为例，如果电梯以加速度g在太空中向上运动，那么电梯内的观察者是无法判断电梯的运动情况。因为此时他感受到的是向下的加速度g，这种情况和在地球表面静止的电梯是一样的。反过来也是一样。因此，强等效原理可以这样表述：“在引力场的任何位置和任何时间都可以找到一个局部惯性系，其中一切的物理定律都与没有引力场时相同。”这里说的局部惯性系可以看成是一个点，它可以忽略掉引力场的不均匀性。有时会把弱等效原理和强等效原理统称为弱等效原理。

甚强等效原理把引力的相互作用也包含在其中，它描述的是引力也不会造成等效原理的破坏。

等效原理的检验

我们前面说过，伽利略在比萨斜塔上进行了自由落体的实验。但是，这个故事只出现在他学生在《伽利略传记》中的追述，没有其余的文献能证明这一点。而且这个实验充满着疑惑：两个大小相差10倍的圆球其空气阻力差别非常大，而且也无法做到同时释放，最后居然得到了完美的结果，因此许多人认为这个故事是杜撰的。

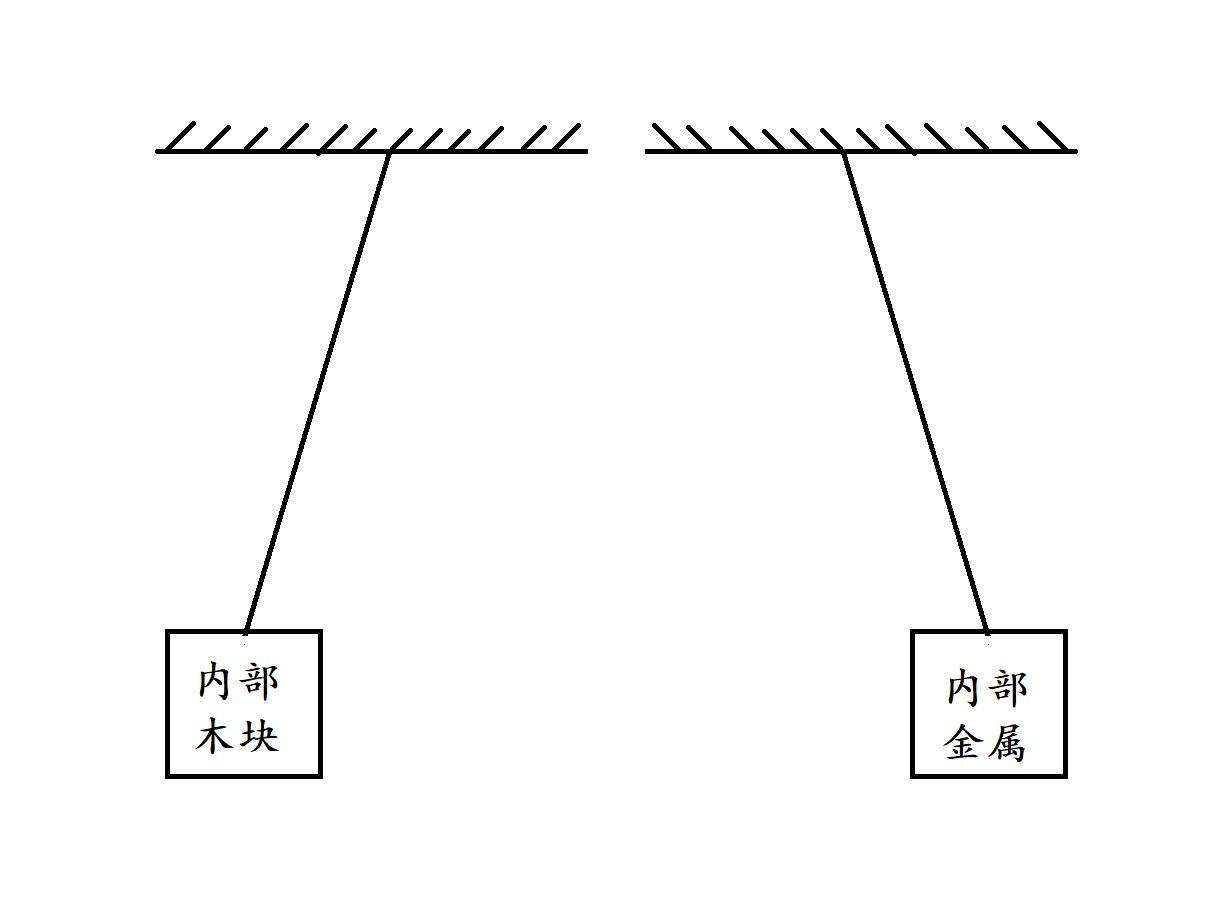
有文献记载的第一个进行实验的是牛顿，他制作了两个一模一样的盒子，里面分别装了相同重量的木块和金属，再把它绑在相同长度的绳子上进行单摆实验。这样做的目的是可以减少空气阻力对实验的影响，并且盒子里的东西还可以进行替换。最后牛顿在千分之一的精度上验证了引力质量和惯性质量之比是与物质无关的常数。

1890年，匈牙利科学家利用扭秤完成了第一个高精度的实验，在10^-9相对精度内证明了引力质量和惯性质量的相等。后来又有三位科学家改进了扭秤实验和测量方法，使精度达到了10^-13量级。这几乎是地面方法的极限了。

后来，人们提出利用卫星来检验等效原理。科学家把两个物体装在卫星之中，如果等效原理不成立，那么这两个物体就会在长年累月的绕地轨道运行中渐渐分开。该计划可以在10^-18的精度内检验该原理。

甚强等效原理的检验

为了统一自然界的四种基本力量，许多人提出了超越广义相对论的理论，例如超弦理论等，这些新理论会对等效原理造成破坏。而上述检验方法的质量太低，自引力太小。要想检验自引力是否能对等效原理造成破坏，需要使用天体来完成实验。

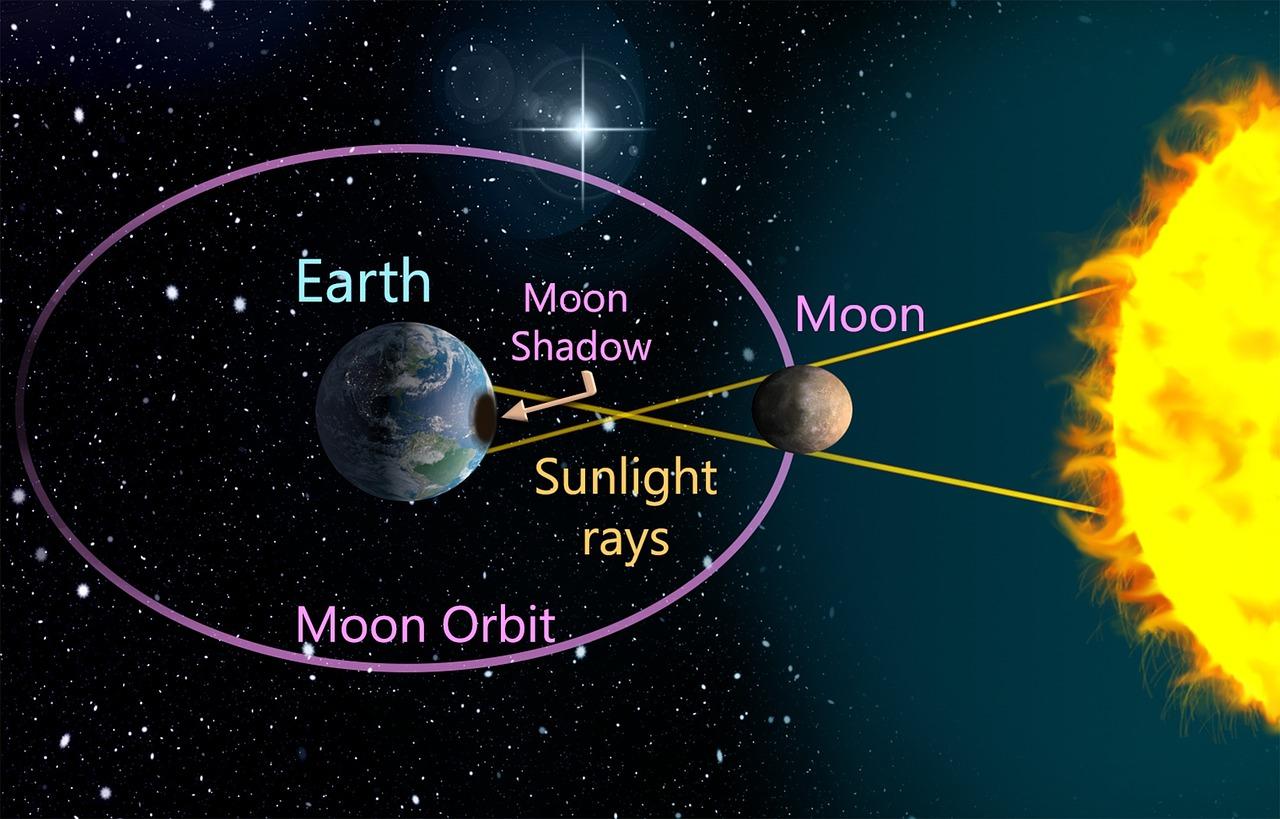
地月系统是人类第一个能完成此实验的天体，如果引力能造成等效原理的破坏，那么地球和月亮在太阳的引力场下加速度会有所不同，月亮绕地球运转的轨道就会出现畸变。冷战期间，前苏联和美国在月球上总共放置了5个反射镜，经过科学家30多年的研究，发现地月轨道没有出现畸变，此实验在10^-13的精度下验证了等效原理并没有被破坏。

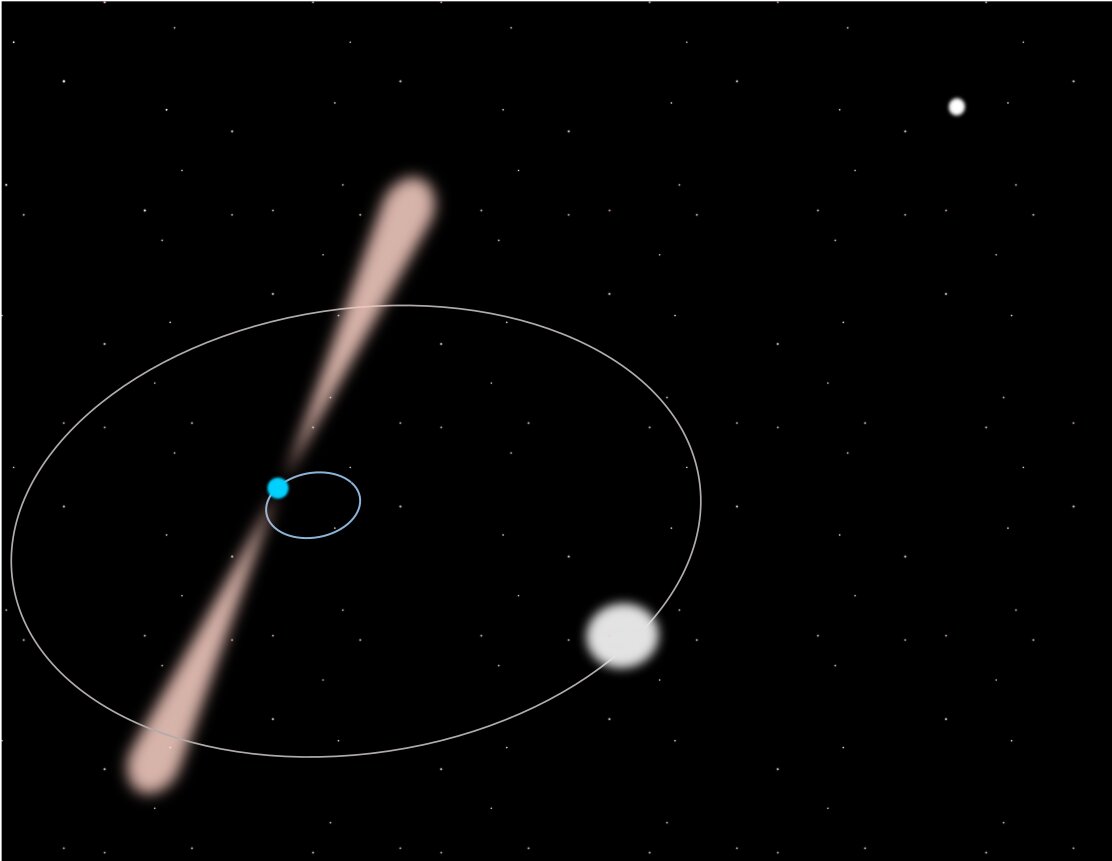
发表在《天文学与天体物理学》杂志上的一项研究也证明了等效原理。来自曼彻斯特大学的研究人员对一个三体系统进行了研究，这个系统包含两颗白矮星和一颗脉冲星。科学家对这三颗星星的位置的追踪达到纳米级别，结果发现脉冲星和白矮星A在白矮星B的重力场下以相同的加速度落向B，从而在一定精度内证明了等效原理的正确性。