分式方程定义是什么（八年级数学上册-分式方程）

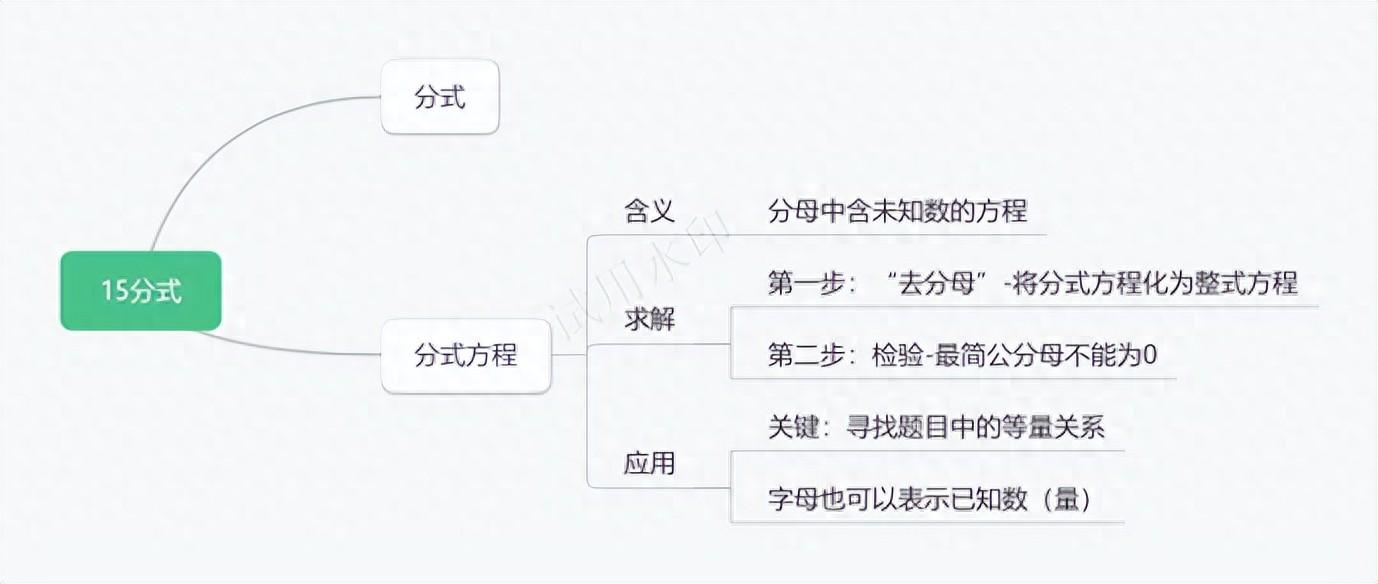
15.3分式方程

一、含义：分母中含未知数的方程叫做分式方程。

二、解分式方程

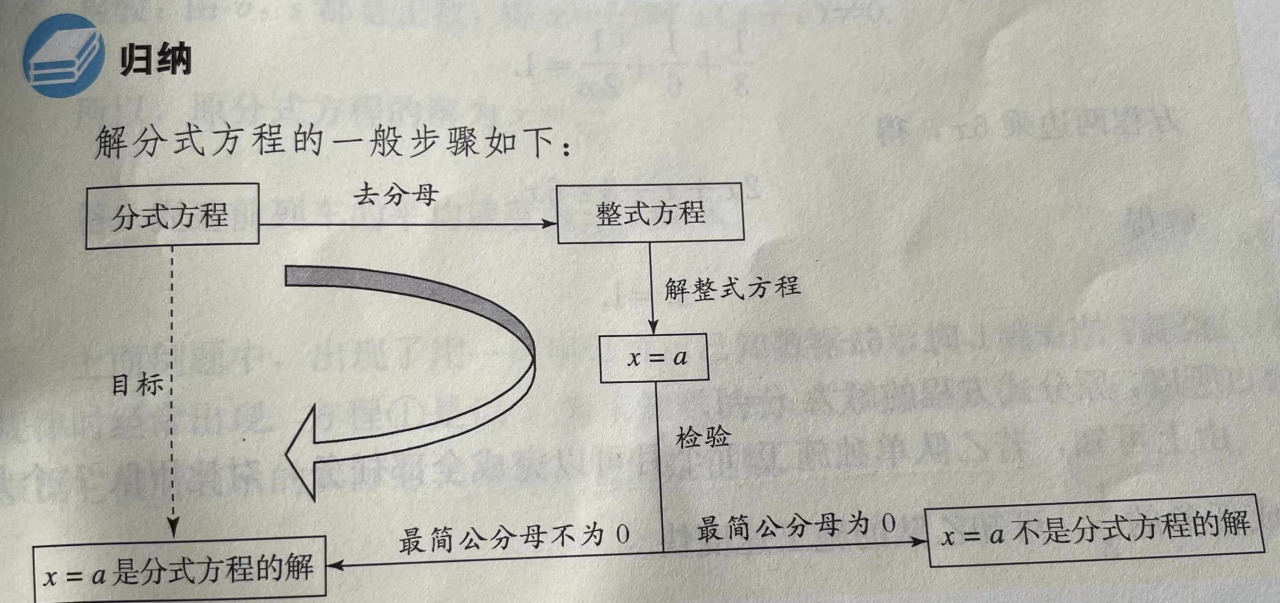
（一）一般方法

1. 基本思路：将分式方程化为整式方程。

2. 具体做法：“去分母”，即方程两边同乘最简公分母。

3. 举例-解方程

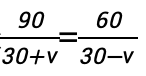
解：方程两边同时乘(30+v)(30-v),得

90(30-v)=60(30+v)

解得v=6

检验：方程的左边=2.5=右边

所以v=6是该方程的解。

（二）检验

解分式方程时，去分母后所得整式方程的解有可能使原方程中分母为0，因此应作如下检验：

将整式方程的解代入最简公分母，如果最简公分母的值不为0，则整式方程的解是原分式方程的解；否则，这个解不是原分式方程的解。

1. 解方程

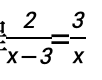
解：方程两边同乘x(x-3),得

2x=3(x-3)

解得x=9

检验：当x=9时，x(x-3)≠0.

所以，原分式方程的解为x=9。

2. 解方程

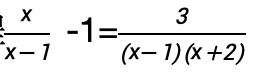
解：等式两边同乘(x-1)(x+2)，得

x(x+2)-(x-1)(x+2)=3

解得x=1

检验：当x=1时，(x-1)(x+2)=0，因此x=1不是该方程的解。

所以该方程无解。

三、分式方程在实际问题中的应用

（一）首先确定：已知条件中哪些等量关系可以用来列方程。

例题：两个工程队共同参与一项筑路工程，甲队单独施工1个月完成总工程的1/3，这时增加了乙队，两队又共同工作了半个月，总工程全部完成。哪个队的施工速度快？

解：甲队单独施工1个月完成总工程的，假设乙队单独施工1个月完成总工程的。

根据题意可得：

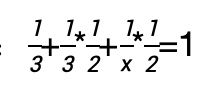
等式两边同乘6x，

解得x=1

检验：当x=1时，6x≠0

所以x=1是该方程的解，即乙队单独施工1个月可以完成总工程的全部。

答：乙队的施工速度快。

（二）表达问题时，用字母不仅可以表示未知数（量），也可以表示已知数（量）。

例题：某次列车平均提速v km/h。用相同的时间，列车提速前行使s km/h，提速后比提速前多行使50km，提速前列车的平均速度为多少？

解：设提速前列车的平均速度为x km/h。（一般都是根据问题设未知数）

根据题意可得

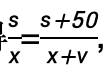
等式两边同乘x(x+v),

解得x=

检验：当x=时，x(x+v)≠0，所以x=是该方程的解。

答：提速前列车的平均速度为 km/h.