电动机与发电机的工作原理是什么?
525次浏览 发布时间:2022-08-26 08:50:09电动机是如何将电能转化为机械能的?发电机又是如何将机械能转化成电能的?8月19日12时,《张朝阳的物理课》第七十九期开播,搜狐创始人、董事局主席兼CEO张朝阳坐镇搜狐视频直播间,先带着网友复习了静电磁学中一系列的重要公式及其应用,接着利用洛伦兹力推导出安培力公式,并讨论了电动机的工作原理。随后,继续利用洛伦兹力推导动生电动势与磁通量变化的关系,并指出感生电动势也满足同样的关系式,统称为法拉第电磁感应定律,该定律可以得到麦克斯韦方程组中关于电场旋度的方程,并帮助人们制造发电机。

静电磁学的特点与总结
张朝阳先回顾了最近这几期关于电磁学的内容,他带领网友先从麦克斯韦方程组出发:
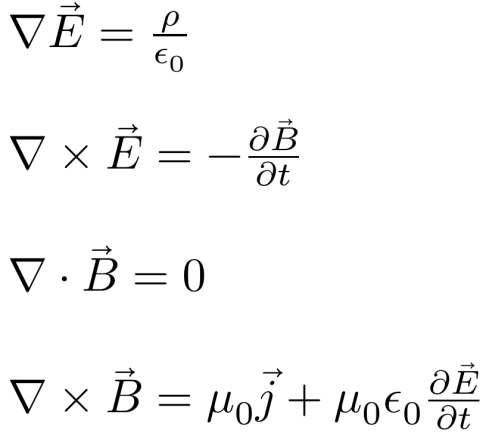
只是简单地推导出电磁波之后,课程就围绕着电磁场不随时间变化的情况展开,这时麦克斯韦方程组中关于时间的偏导项都可以忽略,得到简易的静电磁场方程组:
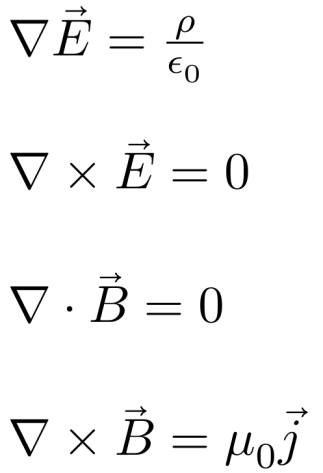
上述静电磁场方程组的解就是库伦定律:
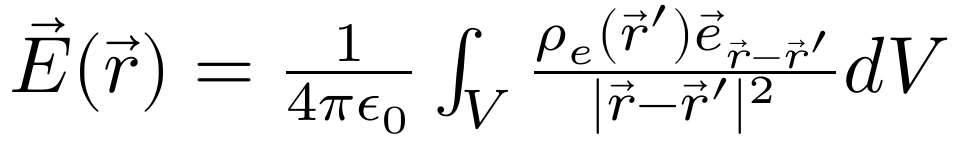
和毕奥萨伐尔定律:
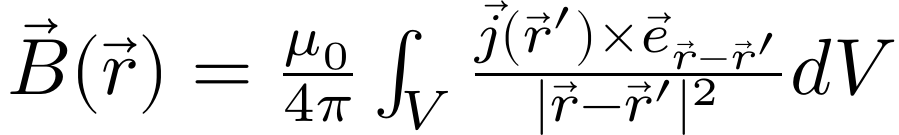
由上述公式可以求出给定恒定电荷密度与电流密度情况下的电磁场。但在对称性较高的情况下,还可以通过静态微分方程组的积分形式来高效求得电磁场。利用散度定理,可以将第一个方程改写为高斯定理:
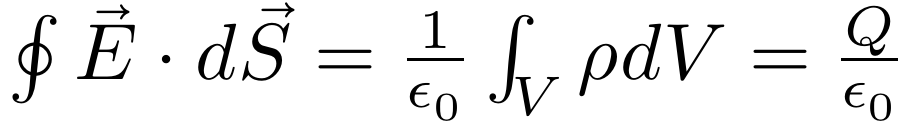
利用高斯定理和对称性,可以简单地得到点电荷,线电荷和面电荷的电场。
同样对第三个公式利用散度定理,也可以得到:
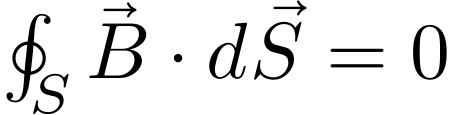
这表明一个闭合曲面的磁通量为零,是磁荷不存在的表现,需要注意的是,该公式对随时间变化的电荷密度与电流密度也成立。
利用斯托克斯公式,第二个方程可以改写为:

这说明电场沿着闭合曲线积分一周后为零,同时也说明将电场从空间某点路径积分到另一点的值与路径无关,所以可以由此定义出标量的势能φ,它满足:

注意,满足上式的势能φ只能在静电磁场的情况下才能被定义出来,否则将与公式-▽×▽φ=▽×E=0矛盾。
同样利用斯托克斯公式,最后一个方程可以改写为:

该公式是安培环路定理,它能代替复杂的毕奥萨伐尔公式来推导磁场。无穷长线电流(导线横截面积可以不趋于零),面电流还有环形电流(例如通电螺线管)等等具有一定对称性的电流密度分布的情况,都可以用安培环路定理简单快速地求得磁场分布。
安培力与电动机
上述回顾的麦克斯韦方程组可知电荷如何产生电磁场,而这节课要讨论的洛伦兹力则可以明白电荷如何受到电磁场的作用,麦克斯韦方程组加上洛伦兹力才构成完整的电磁学理论体系。一个以速度v运动带电量为q的点电荷受到的洛伦兹力为:
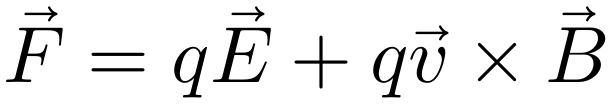
 (张朝阳利用洛伦兹力推导安培力)
(张朝阳利用洛伦兹力推导安培力)
若要考虑的对象不是一个点电荷,而是具有电荷密度ρ的电荷分布。其中一个体积微元dτ具有电荷量q=ρdτ,设此体积微元的运动速度为v,那么它受到的洛伦兹力为:

其中j=ρv是电流密度。将上式两边同除以dτ,得到单位体积受到的洛伦兹力为:
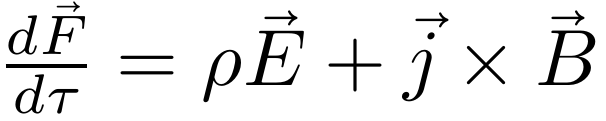
现在只考虑一个简单的情况,忽略掉电场的部分,并且磁场与电流方向垂直,那么单位体积的洛伦兹力的大小可以简写成:
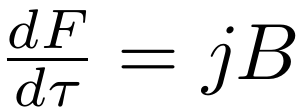
对于横截面积为dS的导线,其电流为:
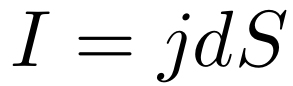
若导线垂直于磁场方向B,则每单位长度的导线受磁场引起的洛伦兹力为:

设导线的长度为L,磁场均匀且垂直于导线,那么导线受力为:

这就是安培力公式,它给出了通电导线在磁场下的受力大小。
利用安培力,可以制作电动机,其构造如下图所示:
 (张朝阳介绍电动机工作原理)
(张朝阳介绍电动机工作原理)
恒定且均匀的磁场B从左向右,一条导线电流垂直纸面向里,另一条导线电流垂直纸面向外,设导线的长度为L,两导线的距离为d,两导线中心的连线与磁场方向的夹角为θ。利用安培力公式,可知两导线受力都为F=BIL。另外F的方向就是j×B的方向,由右手螺旋定则还可判定电流垂直纸面向里的导线受力向下,而电流垂直纸面向外的导线受力向上。由此线圈受到一个沿纸面向外的力矩,并可计算出线圈受到的总力矩为:

其中A=Ld是线圈的面积。
当θ等于零的时候,力矩最大,在力矩的作用下,线圈旋转到θ等于90°的情况,此时力矩为零,当线圈继续转过该平衡位置后,力矩从零增大,但力矩的方向却与之前的相反,阻碍线圈的转动。为了能让力矩始终保持一个方向,可以在θ等于90°的平衡位置处安装一个接口切换装置,使得线圈电流反向,安培力也会反向,使得转过90°之后力矩方向与转过90°之前一致,这样线圈就可以不停地沿着同一方向持续转动,这就是电动机的工作原理,利用安培力将电能转化成机械能。
法拉第电磁感应定律
给放在磁场中的线圈加电动势产生电流后,线圈会转起来,若反过来,使放在磁场中的线圈转起来后,是否会产生电动势呢?
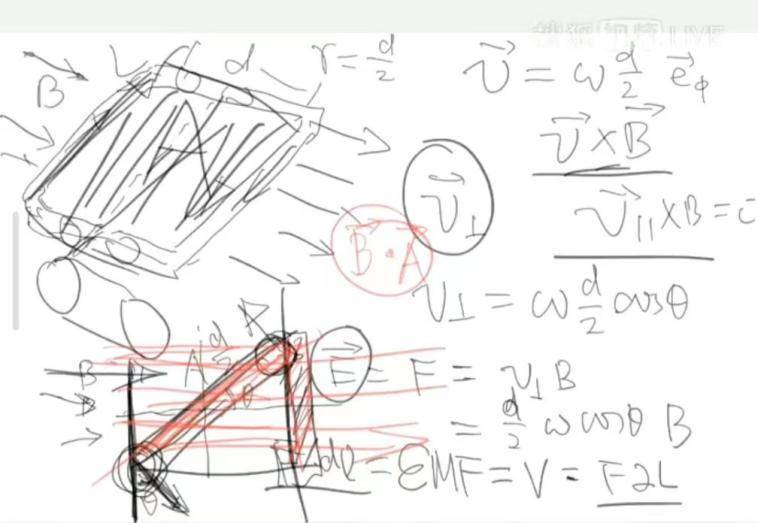 (张朝阳利用洛伦兹力推导感应电动势)
(张朝阳利用洛伦兹力推导感应电动势)
当线圈转起来后,设垂直纸面的导线的运动速度为v,导线中的电荷相对于磁场运动,它们受到的洛伦兹力大小为:
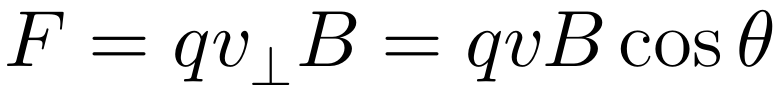
左边的导线的电荷受到洛伦兹力沿导线垂直纸面向外,而右边的导线的电荷受力沿导线垂直纸面向里,由此导线内的电荷会运动形成电流,这说明线圈内产生了电动势。而只有垂直于纸面的两条导线会贡献电动势,线圈内的动生总电动势大小为V,那么由电动势的定义与功的表达式可得:

进一步考虑导线的运动速度v与转动速度ω=dθ/dt之间的关系:

可以得到动生电动势的新表达式:
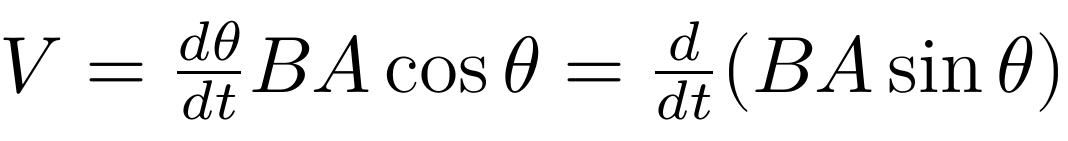
其中面积A=dL。注意到φ=BAsinθ正是线圈的磁通量大小,磁通量方向(定义为磁场垂直于平面的分量)具有向右的分量,从θ=0转到θ=90°的过程中,磁通量逐渐变大,于是磁通量的变化的方向也是具有向右的分量。而根据上述洛伦兹力方向的分析,可知若右手四指朝着电流方向则右手大拇指方向具有向左的分量,表明大拇指方向与磁通量的变化的方向相反。若以右手螺旋定则来联系磁通量方向与电动势的方向,那么具有正负号的动生电动势与磁通量的关系为:
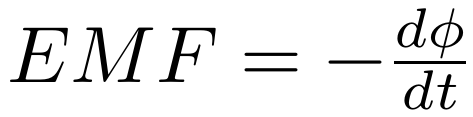
这里动生电动势的产生是由于线圈转动(切割磁感线)引起的,实际上,若线圈不动,但改变磁场的强度也可以产生电动势,称为感生电动势,而感生电动势与磁通量的关系也满足上述公式,电动势与磁通量的关系称为法拉第电磁感应定律。另外,由于线圈不动,所以电荷速度为零,不会受到磁场力qvB,然而电荷还是因为有感生电动势而受力,那根据洛伦兹力公式,电荷受力只能来源于电场力F=qE,即这种情况下磁通量的变化产生了电场,将法拉第电磁感应定律中的感生电动势用电场具体写出来为:
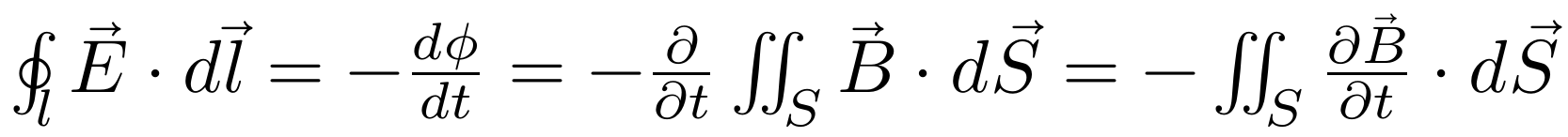
其中最后一个等号用到了线圈不随时间变化的条件。
由于上式对任意线圈成立,所以有:
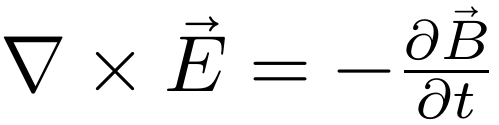
这正是麦克斯韦方程组中关于电场散度的方程。也可以反过来看,该方程能推导出感生电动势与磁通量变化的关系,而洛伦兹力则能推导出动生电动势与磁通量变化的关系,并且神奇的是电动势与磁通量的关系都满足同一方程,这就是大名鼎鼎的法拉第电磁感应定律。安培力使得人们可以制造出电动机,让电能转化为机械能,而法拉第电磁感应定律则反之,让机械能转化成电能,使得人们可以制造出发电机,对人类文明的发展有着重大意义。

