零向量有没有方向和任意向量平行吗？（零向量的方向是任意不确定的？）

人教版A版高中数学必修二改版新教材

零向量的方向是任意的，2020年新人教版A版，高中数学必修二教材上规定“零向量与任一向量平行”。

我们都知道零向量的方向是任意的，那要是说零向量与任意向量垂直是否合适呢？

我的观点是零向量与任意向量垂直也对。但在高中阶段，遇到“零向量与任意向量平行”和“零向量与任意向量垂直”的二选一问题时，应该毫不犹豫地选择“零向量与任意向量平行”。理由如下：

一、课本规定了“零向量与任意向量平行”。

在人教版A版高中数学必修二新版教材，第4页中，“规定零向量与任意向量平行。即对任意向量，都有”。

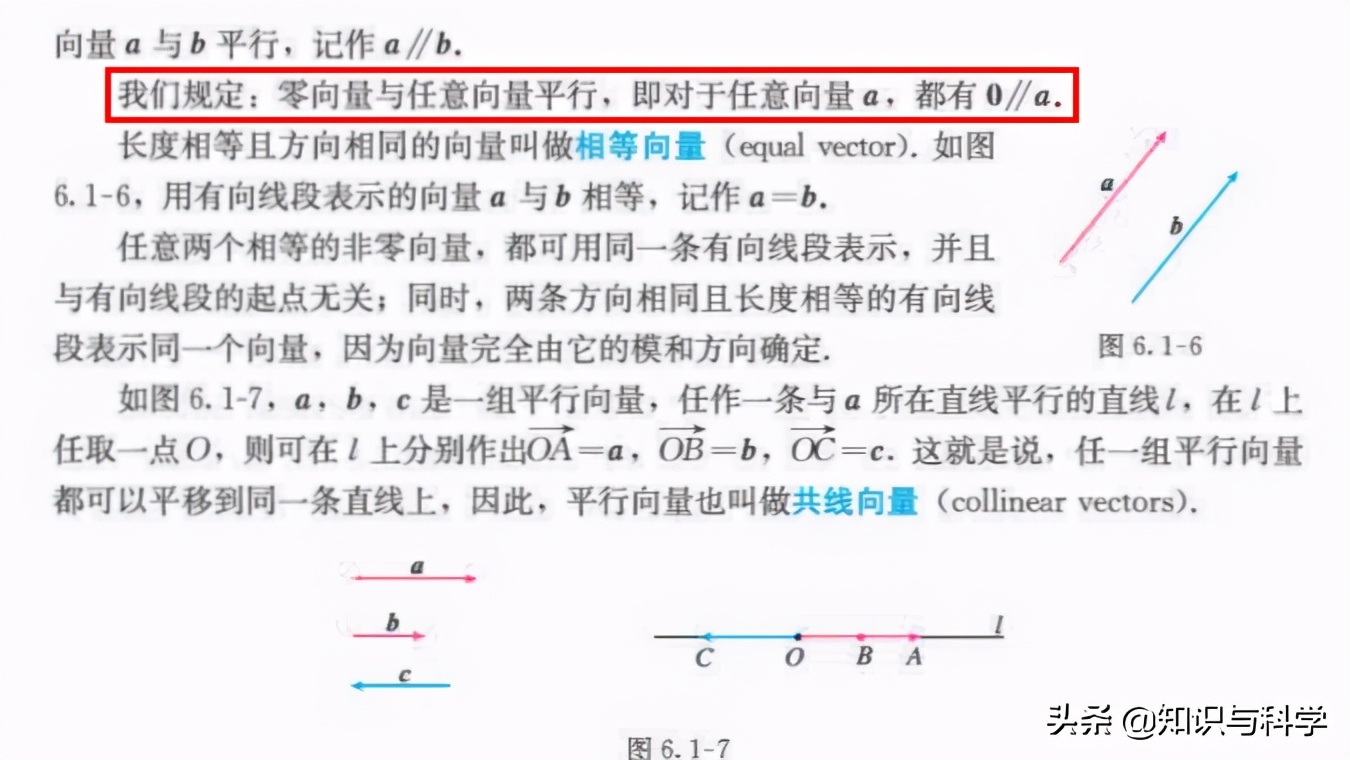
人教版A版高中数学必修二教材第4页

既然是“规定”，那就是要我们“无条件认同”的意思。何况课本上没有任何一处明说或是暗示“零向量与任意向量垂直”这个意思。甚至连“零向量与某个非零向量垂直”这个意思都没有。

二、教材上向量的夹角定义和向量的垂直定义中都不包含零向量。

在人教版A版高中数学必修二新版教材，第17页中。定义两个向量的夹角时，教材明确强调了“两个非零向量”。这就是在告诉我们，讨论零向量和任意向量的夹角问题是不合适的。所以，虽然零向量方向任意，但说零向量与任意非零向量的夹角是90度也是不合理的。

人教版A版高中数学必修二教材第17页

教材在17页给出了两个非零向量的数量积（内积）的定义后，接着又作出了一个规定：“规定零向量与任意向量的数量积为0”.

也许你会感觉到这点是多余的，你应该觉得既然零向量的模为0，直接带入向量数量积的定义式中也能得到0，为什么要“多此一举”地做个规定是0呢？原因就是，零向量的夹角（平行、垂直）和数量积是个单独而特殊的存在，讨论零向量的数量积是没意义的。

对于特殊情况，我们只能特殊对待，也就有了我们对零向量的两个规定。“规定零向量与任意向量平行”和“规定零向量与任意向量的数量积为0”.

综上，网上有许多都认为“零向量与任意向量垂直”成立，这自有其一定道理和依据。

但因为教材上的“规定”，我觉得考试时遇到让我们在“零向量和任意向量平行”和“零向量和任意向量垂直”的问题中二选一时，我们还是应该毫不犹豫的选择“零向量与任意向量平行”。

大家如果有别的见解和看法，欢迎在下方留言讨论。

编者注：可以肯定地说，关于“零向量的平行和垂直”问题基本不会在高考中出现。本文只是对课外辅导书中可能会遇到的这个“偏、难、怪”题的一般化讨论。大家记住课本上明确规定的结论，对“零向量的平行和垂直问题”当成数学的业余兴趣即可。不必花费太多精力纠结这个问题，以免影响考试备考。